Question 1.
The probability of picking a red sweet from a bag is 0.05.
Find the probability of not picking a red sweet. [1] (0580/23/M/J/22)
Question 2.
The diagram shows 11 cards.

(i) One of these cards is chosen at random. Write down the probability that the letter on the card is not A. [1]
(ii) A card is chosen at random from these 11 cards and then replaced. A second card is then chosen at random.
Find the probability that exactly one card has the letter N. [3]
Question 3.
50 students are asked if they like English (E) and if they like mathematics (M).
3 say they do not like English and do not like mathematics.
33 say they like English.
42 say they like mathematics.
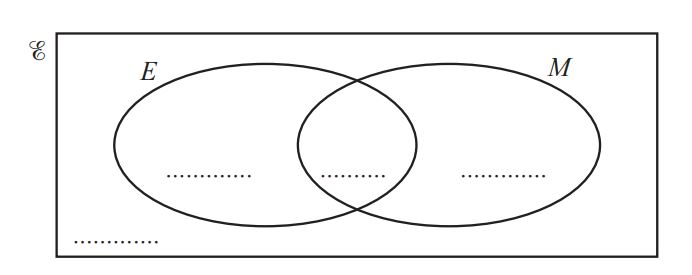
(i) Complete the Venn diagram. [2]
(ii) A student is chosen at random. Find the probability that this student likes English and likes mathematics. [1]
(iii) Two students are chosen at random. Find the probability that they both like mathematics. [2]
(iv) Two students who like English are chosen at random. Find the probability that they both also like mathematics. [2]
Question 4.
The probability that Shalini is late for school on any day is 1/6.
(i) Complete the tree diagram for Monday and Tuesday. [1]
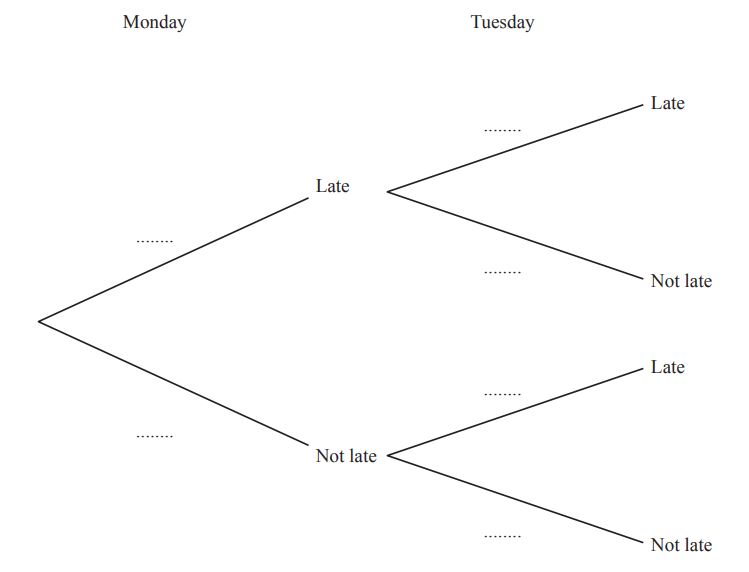
(ii) Calculate the probability that Shalini is late on Monday but is not late on Tuesday. [2]
Question 5.
The Venn diagram shows the number of students in a group of 50 students who wear glasses (G), who wear trainers (T ) and who have a mobile phone (M ).
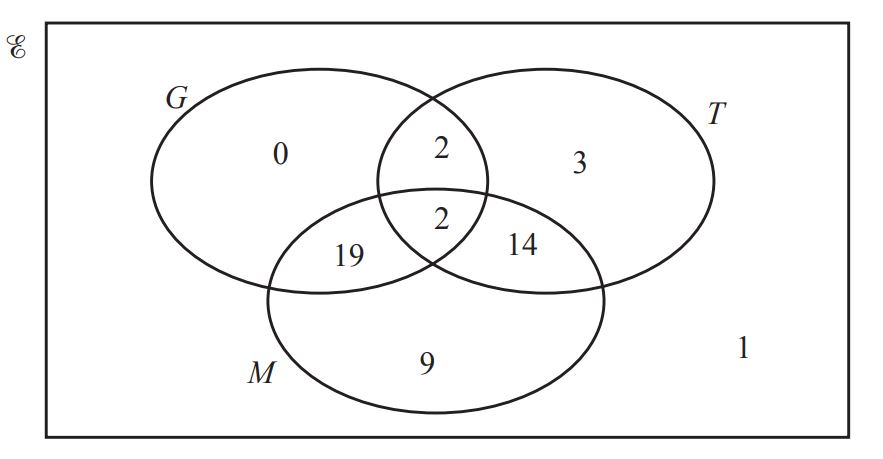
(i) Use set notation to describe the region that contains only one student. [1]
(ii) Find 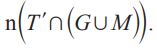 [1]
[1]
(iii) One student is picked at random from the 50 students. Find the probability that this student wears trainers but does not wear glasses. [1]
(iv) Two students are picked at random from those wearing trainers. Find the probability that both students have mobile phones. [3]
Question 6.
In a class activity, all the 15 students wear hats. 7 students wear red hats, 6 students wear green hats and 2 students wear white hats.
(i) One of these students is picked at random. Find the probability that this student wears a red hat. [1]
(ii) Two of the 15 students are picked at random. Show that the probability that these two students wear hats of the same colour is 37/105. [3]
(iii) Three of the 15 students are picked at random. Find the probability that at least two of these three students wear red hats. (0580/42/F/M/21)
Question 7.
The probability that Jane wins a game is 7/10 .
(a) Find the probability that Jane does not win the game. [1]
(b) Jane plays this game 50 times. Find the number of times she is expected to win the game. [1] (0580/22/M/J/21)
Question 8.
Malik goes to a shop every day to buy bread.
On any day, the probability that Malik goes to the shop in the morning is 0.7 .
If he goes in the morning, the probability that there is bread for Malik to buy is 0.95 .
If he goes later, the probability that there is bread for Malik to buy is 0.6.
Calculate the probability that, on any day, there is bread for Malik to buy. [3] (0580/23/M/J/21)
Question 9.
The Venn diagram shows the number of students in a group of 30 who have brothers (B ),
sisters (S ) or cousins (C ).
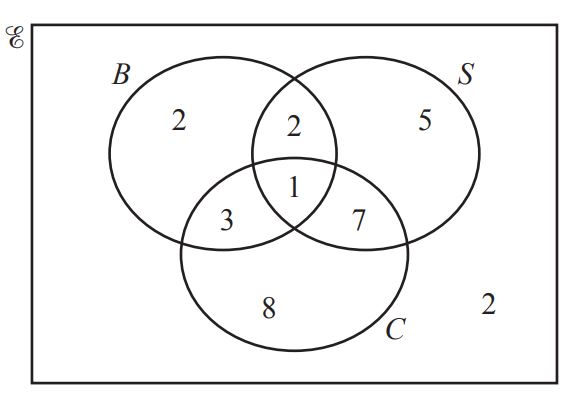
(i) Write down the number of students who have brothers. [1]
(ii) Write down the number of students who have cousins but do not have sisters. [1]
(iii) Find 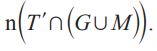 [1]
[1]
(iv) Use set notation to describe the set of students who have both cousins and sisters but do not have brothers. [1]
(v) One student is picked at random from the 30 students. Find the probability that this student has cousins. [1]
(vi) Two students are picked at random from the students who have cousins.
Calculate the probability that both these students have brothers. [3]
(vii) One student is picked at random from the 30 students.
Event A This student has sisters.
Event B This student has cousins but does not have brothers.
Explain why event A and event B are equally likely. [1] (0580/41/M/J/21)
Question 10.
In a class of 24 students, 18 students like homework (H ), 15 students like tests (T ) and 1 student does not like homework and does not like tests.
(a) Complete the Venn diagram to show this information. [2]
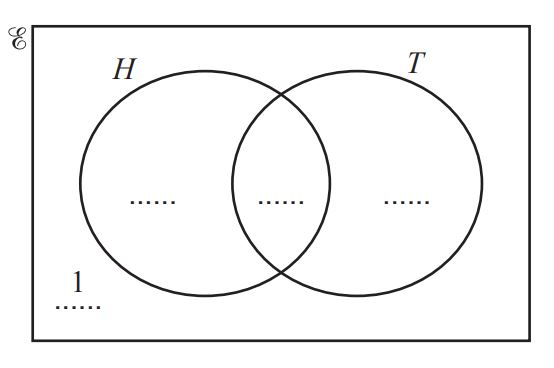
(b) Write down the number of students who like both homework and tests. [1]
(c) Find 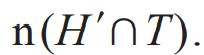 [1]
[1]
(d) A student is picked at random from the class. Write down the probability that this student likes tests but does not like homework. [1]
(e) Two students are picked at random from the class.
Find the probability that both students do not like homework and do not like tests. [1]
(f) Two of the students who like homework are picked at random. Find the probability that both students also like tests. [3] (0580/43/M/J/21)
Question 11.
Katy has 5 white flowers, x red flowers and (2x+1) yellow flowers.
She picks a flower at random.
The probability that it is white is 1/12.
Find the probability that it is yellow. [4] (0580/22/O/N/21)
Question 12.
Sarah spins a fair four-sided spinner numbered 0, 1, 1 and 3.
(i) What number is the spinner most likely to land on? [1]
(ii) Sarah spins the spinner twice.
Find the probability that it lands on the number 1 both times. [2]
(iii) Sarah spins the spinner until it lands on the number 3.
The probability that this happens on the nth spin is 729/16384.
Find the value of n.
n = ………………………………………… [2] (0580/43/O/N/21)
Question 13.
Scott takes an examination.
The examination is in two parts, a theory test and a practical test.
Both parts must be passed to pass the examination.
The probability that Scott passes the theory test is 0.9 .
The probability that Scott passes the practical test is 0.8 .
Find the probability that
(i) Scott passes the examination, [2]
(ii) Scott passes the theory test or the practical test but not both. [3] (0580/43/O/N/21)
*Solutions
Click here to view the topic wise solutions for the problems above.
