Question 1.

The Venn diagram shows the number of students in a group of 30 who have brothers (B ), sisters (S ) or cousins (C ). (0580/41/M/J/21)

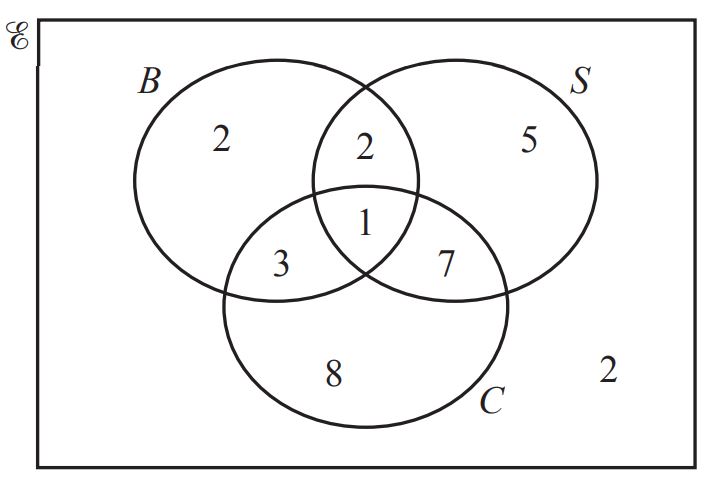
(i) Write down the number of students who have brothers. [1]

(ii) Write down the number of students who have cousins but do not have sisters. [1]

(iii) Find [1]

(iv) Use set notation to describe the set of students who have both cousins and sisters but do not
have brothers. [1]

(v) One student is picked at random from the 30 students.

Find the probability that this student has cousins. [1]

(vi) Two students are picked at random from the students who have cousins.

Calculate the probability that both these students have brothers. [3]

(vii) One student is picked at random from the 30 students.

Event A This student has sisters.
Event B This student has cousins but does not have brothers.

Explain why event A and event B are equally likely. [1]

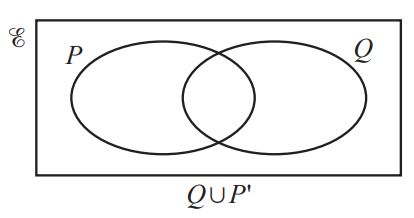
Question 2.

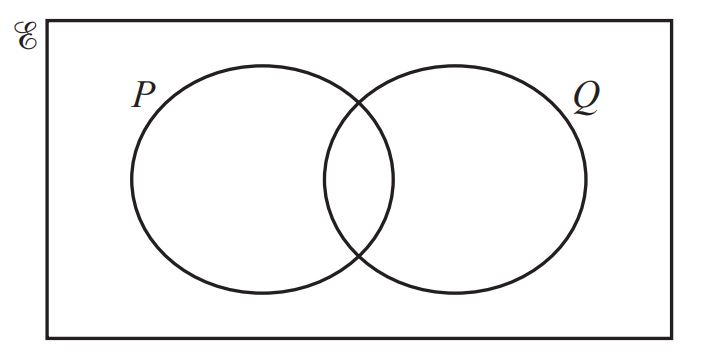
a) In the Venn diagram, shade the region P’ ∪ Q. [1] (0580/41/M/J/21)

(b) There are 50 students in a group.

34 have a mobile phone (M ).
39 have a computer (C ).
5 have no mobile phone and no computer.

Complete the Venn diagram to show this information. [2] (0580/41/M/J/21)

Question 3.

In a class of 24 students, 18 students like homework (H ), 15 students like tests (T ) and 1 student does
not like homework and does not like tests. (0580/43/M/J/21)

(a) Complete the Venn diagram to show this information.

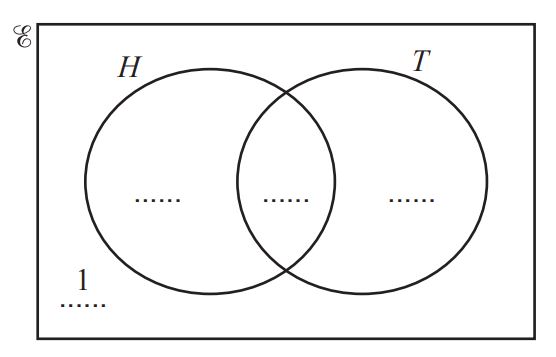
(b) Write down the number of students who like both homework and tests. [1]

(c) Find n(H’ ∩ T).

(d) A student is picked at random from the class.

Write down the probability that this student likes tests but does not like homework. [1]

(e) Two students are picked at random from the class.

Find the probability that both students do not like homework and do not like tests. [1]

(f) Two of the students who like homework are picked at random.

Find the probability that both students also like tests. [3]

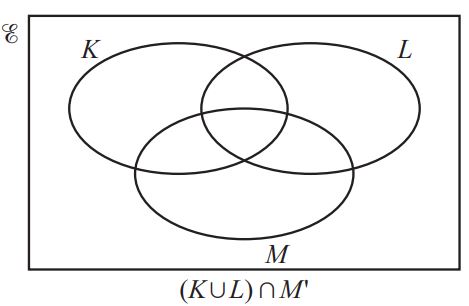
Question 4.

In these Venn diagrams, shade the given regions.

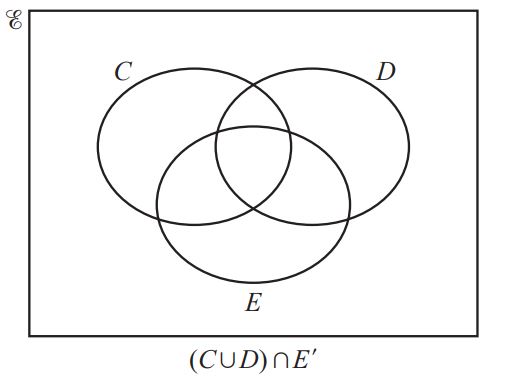
Question 5.

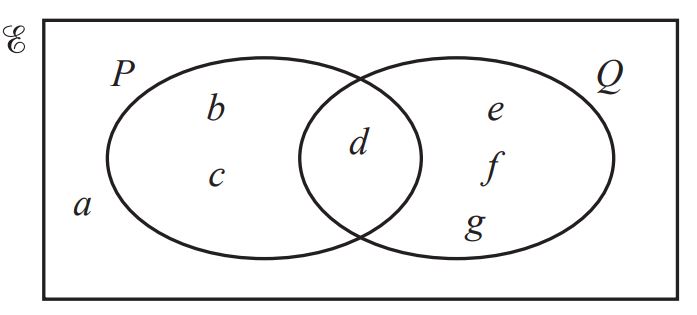
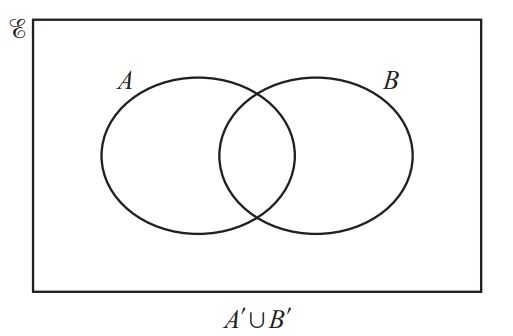
(a) Complete the statement.

P∪Q = {  } [1]

(b) Find n(Q).  [1]

(c) Find n(P ∩ Q ). [1]

Question 6.

The Venn diagram shows the number of students in a class of 40 who study physics (P), mathematics (M) and geography (G). (0580/22/M/J/22)

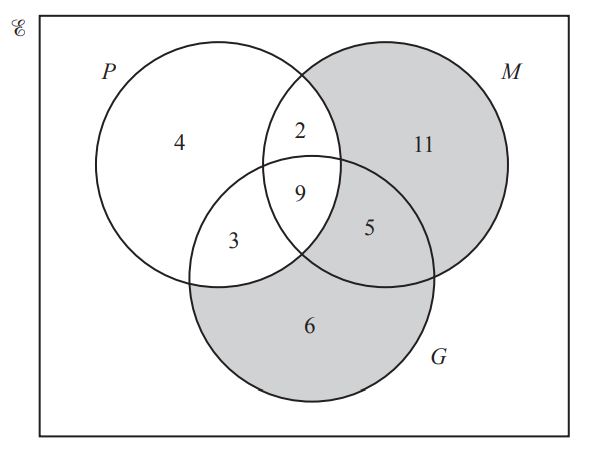
(a) Use set notation to describe the shaded region. [1]

(b) Find n((P ∩ G) ∪ M’) . [1]

(c) A student is chosen at random from those studying geography.

Find the probability that this student also studies physics or mathematics but not both. [2]

Question 7.

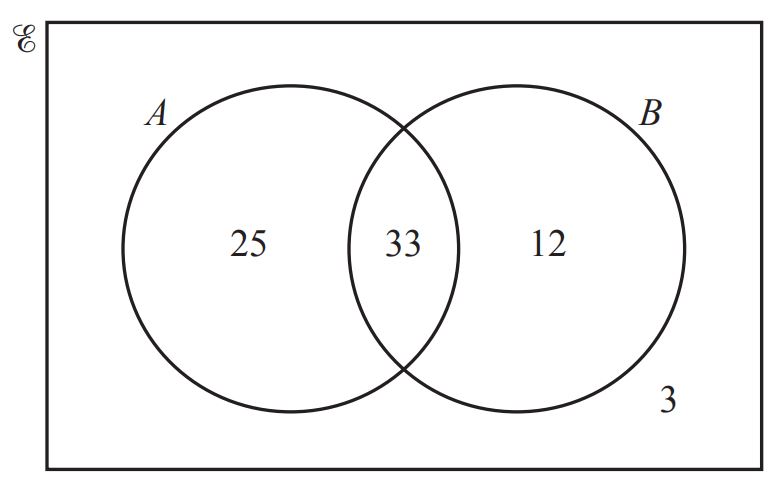
Find n(A ∩ B)’. [1]  (0580/23/M/J/22)

Question 8.

(i) Use set notation to describe the shaded region in the Venn diagram. [1] (0580/41/M/J/22)

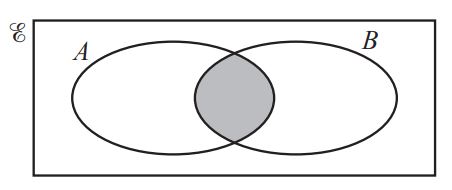
(ii) Shade the correct region in each Venn diagram. [2]

Question 9.

The Venn diagram shows the number of students in a group of 50 students who wear glasses (G), who wear trainers (T  ) and who have a mobile phone (M  ).

(i) Use set notation to describe the region that contains only one student. [1]

(ii) Find n(T’ ∩ (G ∪ M)) [1]

(iii) One student is picked at random from the 50 students. [1]

Find the probability that this student wears trainers but does not wear glasses. [1]

(iv) Two students are picked at random from those wearing trainers.

Find the probability that both students have mobile phones. [3]

Question 10.

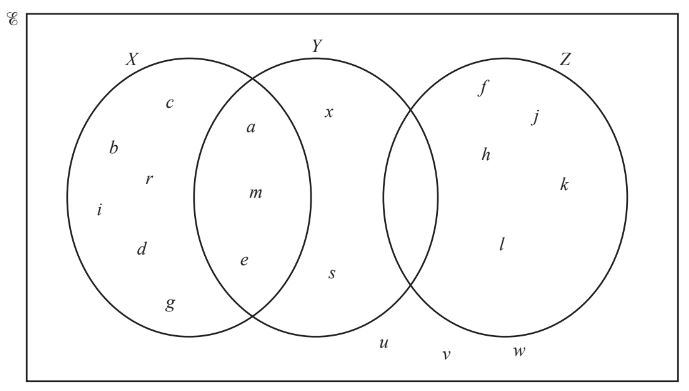
(a) Use set notation to complete the statements for the Venn diagram above.

(i) c ……………….. X [1]

(ii) ……………………………. = { a, m, e } [1]

(iii) Y ∩  k = ……………………………. [1]

(b) List the elements of (X ∪ Y ∪ Z)’

…………………………………………… [1]

(c) Find n(X’ ∩  Z) [1]

Question 11.

On another day, the number of members using the exercise machines (E), the swimming pool (S) and
the tennis courts (T) is shown on the Venn diagram.

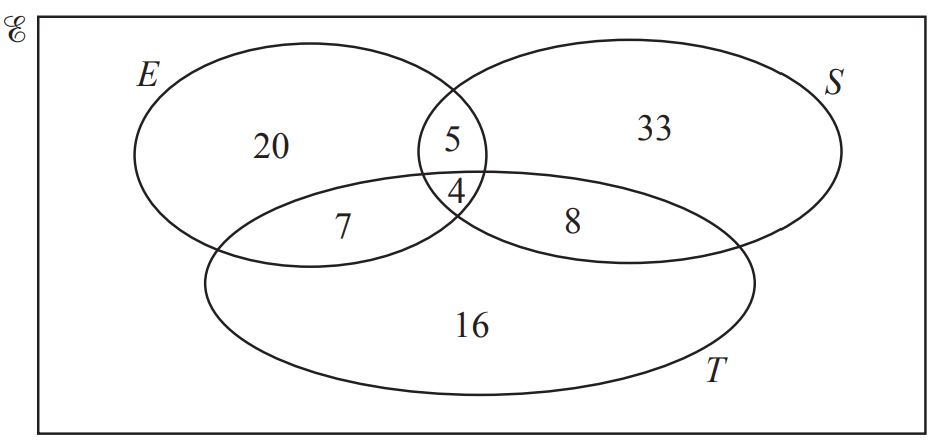
(i) Find the number of members using only the tennis courts. [1]

(ii) Find the number of members using the swimming pool. [1]

(iii) A member using the swimming pool is chosen at random.
Find the probability that this member also uses the tennis courts and the exercise machines. [2]

(iv) Find n(T ∩ (E ∪ S)).  [1] (0580/41/M/J/18)

Question 12.

The Venn diagram shows information about the number of elements in sets A, B and ξ.

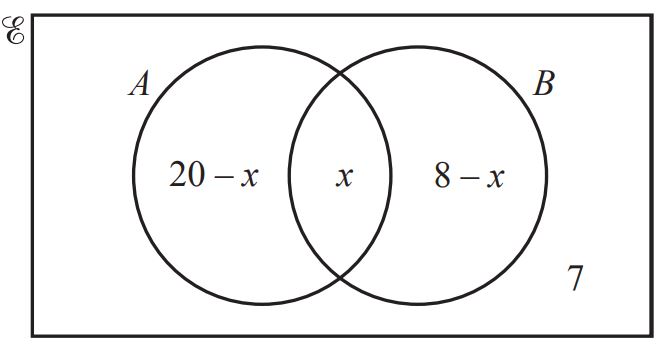
(a) n(A∪ B) = 23

Find the value of x.
x = ………………………………………… [3]

(b) An element is chosen at random from ξ.
Find the probability that this element is in (A ∪  B)’. [2] (0580/22/M/J/18)

Question 13.

(a) M = { x: x is an integer and 2<=x<6 }

(i) Find n(M). [1]

(ii) Write down a set N where .
{………………………………………….. } [1]

(b) In each Venn diagram, shade the required region. [2]

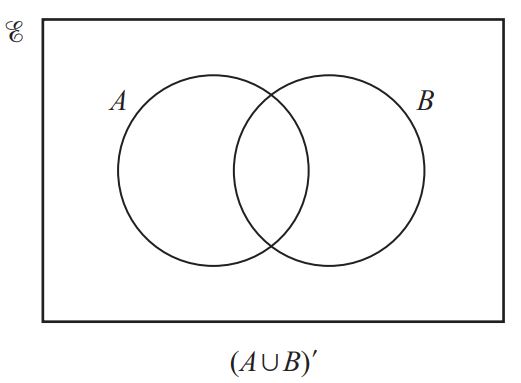
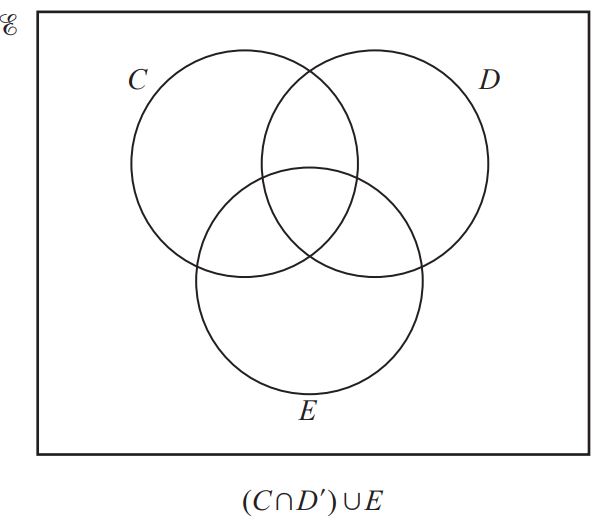
 Question 14.

(a) The Venn diagram shows two sets, A and B. (0580/42/F/M/19)

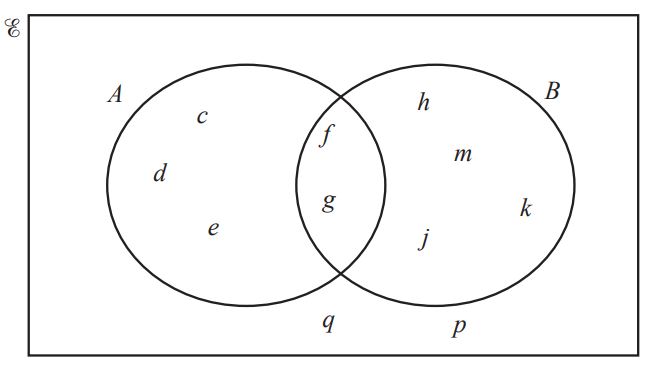
(i) Use set notation to complete the statements.

(a) d ………………. A [1]

(b) {f, g} = …………………………. [1]

(ii) Complete the statement.
n (…………………….) = 6 [1]

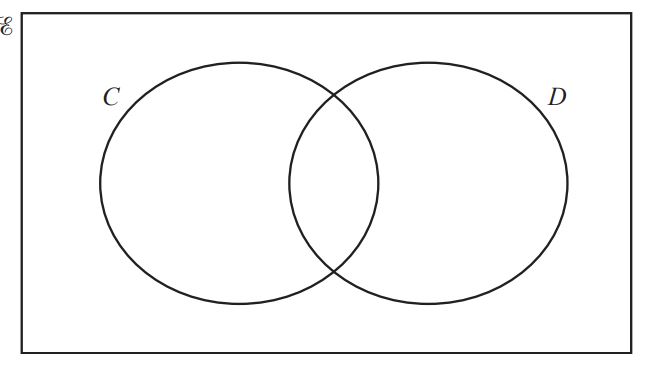
(b) In the Venn diagram below, shade C ∩ D’.

Question 15.

(c) 50 students study at least one of the subjects geography (G), mathematics (M) and history (H).

18 study only mathematics.
19 study two or three of these subjects.
23 study geography.

The Venn diagram below is to be used to show this information.

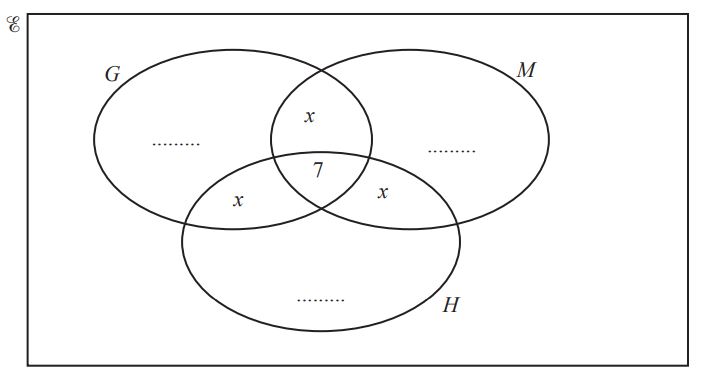
(i) Show that x = 4. [2]

(ii) Complete the Venn diagram. [2]

(iii) Use set notation to complete this statement.
(G ∪  M ∪ H)’ = ………………….. [1]

(iv) Find n((G ∪ M ∪ H )). [1]

Question 16.

Σ = {students in a school}
F = {students who play football}
B = {students who play baseball}
There are 240 students in the school.
• 120 students play football
• 40 students play baseball
• 90 students play football but not baseball.

(a) Complete the Venn diagram to show this information.

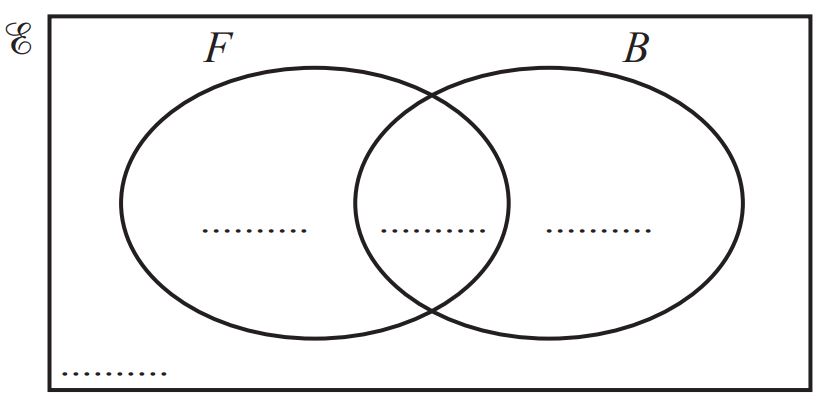
(b) Find n(F’ ∩ B’). [1]
(c) A student in the school is chosen at random.

Find the probability that this student plays baseball but not football. [1]

(d) Two students who play baseball are chosen at random.

Find the probability that they both also play football. [3]