Coordinate Geometry Past Paper Questions (AS & A Level)

Question 1

The circle with equation (x + 1)² + (y-2)² = 85 and the straight line with equation y = 3x − 20 are shown in the diagram. The line intersects the circle at A and B, and the centre of the circle is at C. (9709/12/F/M/22)

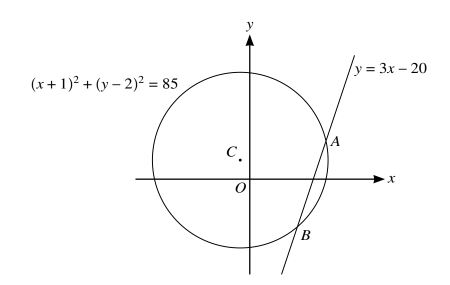
(a) Find, by calculation, the coordinates of A and B. [4]

(b) Find an equation of the circle which has its centre at C and for which the line with equation
y = 3x − 20 is a tangent to the circle. [4]

Question 2

The equation of a circle is x² + y² + 6x − 2y − 26 = 0. (9709/11/M/J/22)

(a) Find the coordinates of the centre of the circle and the radius. Hence find the coordinates of the lowest point on the circle. [4]

(b) Find the set of values of the constant k for which the line with equation y = kx − 5 intersects the circle at two distinct points. [6]

Question 3

The equation of a circle is x² + y² + ax + by − 12 = 0. The points A (1, 1) and B (2, −6) lie on the circle.

(a) Find the values of a and b and hence find the coordinates of the centre of the circle. [4]

(b) Find the equation of the tangent to the circle at the point A, giving your answer in the form px + qy = k, where p, q and k are integers. [4]

Question 4

The diagram shows the circle with equation (x − 2)² + (y + 4)² = 20 and with centre C. The point B has coordinates (0, 2) and the line segment BC intersects the circle at P. (9709/13/M/J/22)

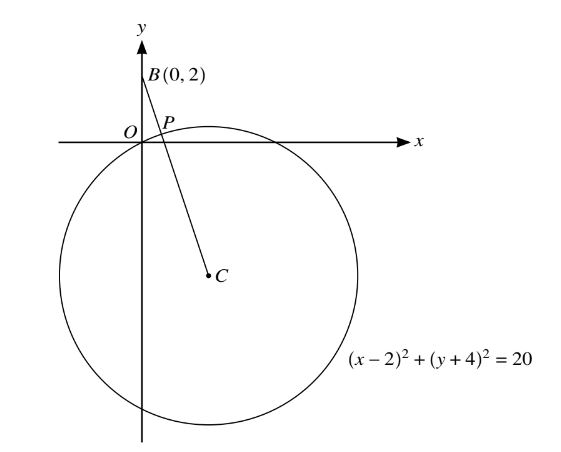
(a) Find the equation of BC. [2]

(b) Hence find the coordinates of P, giving your answer in exact form. [5]

Question 5

The points A (7, 1), B (7, 9) and C (1, 9) are on the circumference of a circle. (9709/12/F/M/21)

(a) Find an equation of the circle. [5]

(b) Find an equation of the tangent to the circle at B. [2]

Question 6

The equation of a circle is x² + y² − 4x + 6y − 77 = 0.

(a) Find the x-coordinates of the points A and B where the circle intersects the x-axis. [2]

(b) Find the point of intersection of the tangents to the circle at A and B. [6]

Question 7

Points A and B have coordinates (8, 3) and (p, q) respectively. The equation of the perpendicular bisector of AB is y=−2x+4. (9709/12/M/J/21)

Find the values of p and q. [4]

Question 8

Points A (−2, 3), B (3, 0) and C (6, 5) lie on the circumference of a circle with centre D. (9709/13/M/J/21)

(a) Show that angle ABC = 90°. [2]

(b) Hence state the coordinates of D. [1]

(c) Find an equation of the circle. [2]

The point E lies on the circumference of the circle such that BE is a diameter.

(d) Find an equation of the tangent to the circle at E. [5]

Question 9

The point A has coordinates (1, 5) and the line l has gradient -2/3 and passes through A. A circle has centre (5, 11) and radius √52. (9709/12/M/J/21)

(a) Show that l is the tangent to the circle at A. [2]

(b) Find the equation of the other circle of radius √52 for which l is also the tangent at A. [3]